Lois de Kepler

Claude Ptolémée (IIè siècle après J.-C.) fut le premier à décrire avec précision le mouvement du Soleil, de la Lune et des planètes autour de la Terre, considérée alors comme le centre du monde, par une combinaison de mouvements circulaires uniformes […]. Trois siècles plus tard, Nicolas Copernic (1473-1543), astronome polonais, propose son modèle héliocentrique du système solaire, comprenant des combinaisons de trajectoires circulaires mais encore plus compliquées que celles de Ptolémée.

1ère loi : Loi des orbites (1609)

Les mesures très précises de Mars faites par l’astronome danois Tycho Brahe (1546-1601), convainquent son élève Johannes Kepler (1571-1630), astronome allemand (voir doc.2), que l’orbite de la planète rouge ne peut pas être décrite ni par un cercle, ni par une combinaison de cercles, mais qu’elle est elliptique, le Soleil occupant l’un des foyers. Il publie ce résultat en 1609, dans son Astronomia nova, aujourd’hui connu sous le nom de première loi de Kepler.

Important

Dans le référentiel héliocentrique, la trajectoire d’une planète est une ellipse dont le Soleil occupe l'un des foyers.

Propriétés d'une éllipse - source : LeLivreScolaire

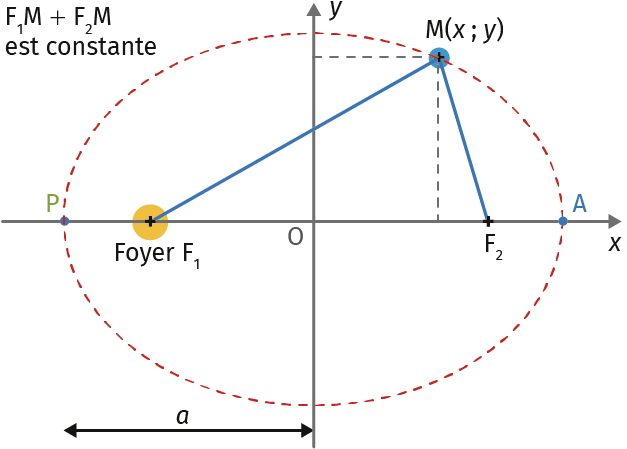
• a : demi grand-axe.
• P : La position la plus proche du Soleil est le périhélie.
• A : la position la plus éloignée du Soleil est l’aphélie.

Remarques

• Il ne faut pas confondre périhélie et aphélie avec périgée et apogée, qui sont les termes équivalents pour des satellites de la Terre.
• Un cercle est une ellipse particulière pour laquelle les deux foyers F et F’ sont confondus et situés en O. Dans ce cas, relation $F_{1}M+F_{2}M=\text{constante}$ devient $OM=R$, où $R$ est le rayon du cercle.
• Dans la réalité, les orbites des planètes du système solaire sont des ellipses qui ressemblent beaucoup à des cercles.

2ème loi : Loi des aires (1609)

Puis, il généralise cette loi à d’autres planètes dans ses Epitome astronomiae copernicanae (entre 1618-1621) où apparait la première description correcte du système solaire et dans lesquelles est correctement formulée la deuxième loi de Kepler : Pendant des durées égales, le rayon Soleil-Planète balaye des aires égales.

Important

Le segment reliant le Soleil à la planète balaie des aires égales pendant des durées égales.

Lois des aires - source : Maxicours

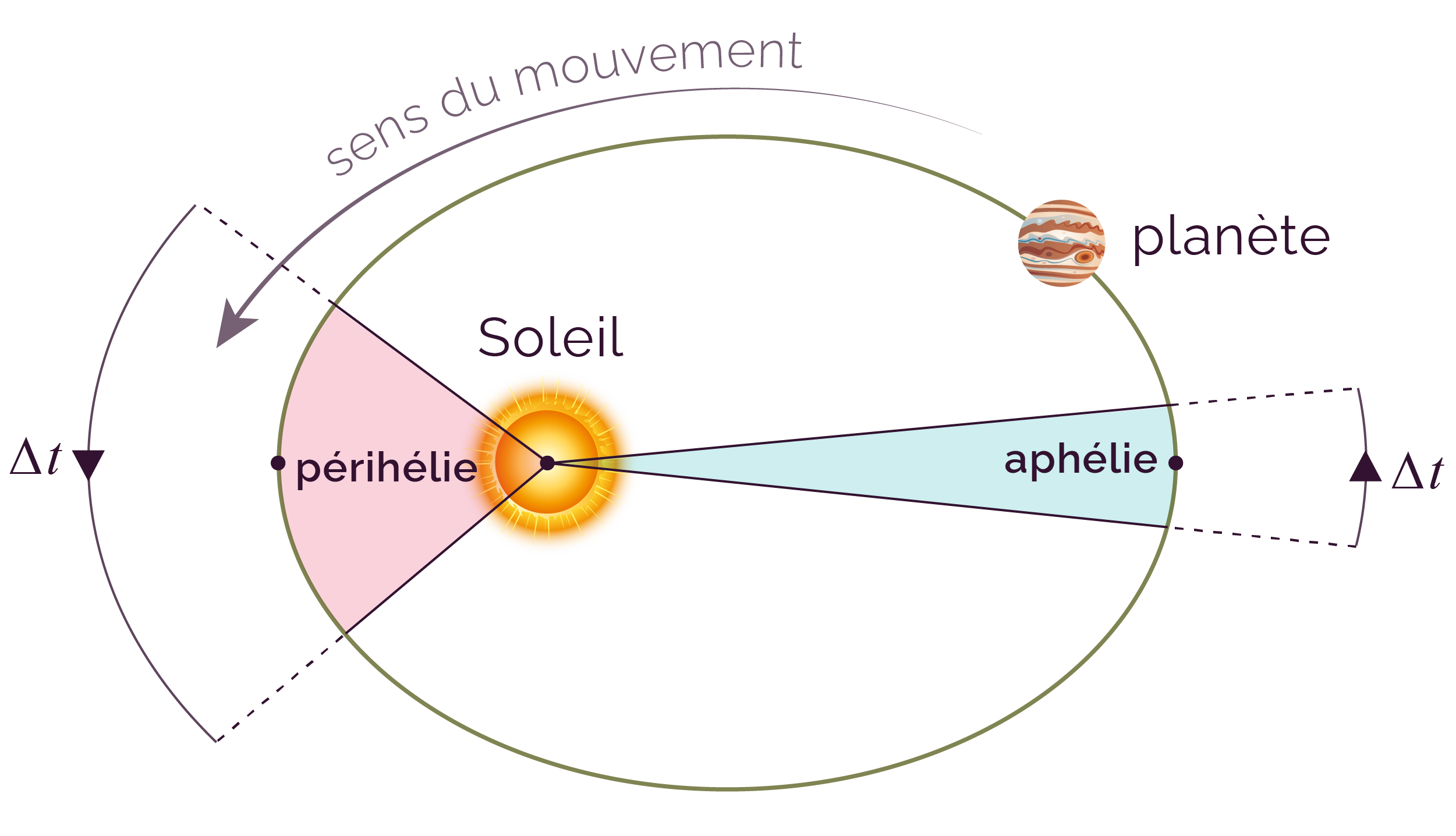
On observe que sur le schéma que les aires sont égales pendant des durée $\mathrm{\Delta }t$ égales. On observe ainsi que plus la planète est proche du Soleil, plus la distance parcourue pendant une durée $\mathrm{\Delta }t$ est grande. Ainsi on en déduit aisément que la vitesse de révolution est d'autant plus élevée que la planète est proche de la périhélie.

Par exemple, pour une étoile en orbite autour d'un trou noir, on peut déterminer la position du trou noir. Par définition le trou noir n'est pas visible mais on peut déterminer sa position grâce à la trajectoire élliptique d'une étoile et sa vitesse de révolution autour du trou noir. Grâce à ces mesures on peut déterminer la périhélie et donc le foyer de l'éllipse où se situe le trou noir.

3ème loi : Loi des périodes (1618)

En 1619, dans Harmonice mundi, il établit la troisième loi de Kepler.

Important

Le carré de la période de révolution T d'une planète autour du Soleil est proportionnel au cube de la longueur a du demi grand axe de son orbite.

$$\frac{T^2}{a^3}=\text{constante}$$

Attention

Ne pas confondre la période de révolution avec la période de rotation (sur elle-même) d'une planète.

Par exemple, on estime, pour la Terre :

• période rotation : 24 h ;
• période de révolution : 365,25 jrs.

Remarques

Les trajectoires de faible excentricité peuvent être modélisées par des cercles. La 3ème loi de Kepler s’ecrit alors :

$$\frac{T^2}{R^3}=\text{constante}$$

Limites d'application des lois de Kepler

Les lois de Kepler sont valables pour tout objet, satellite ou planète en orbite autour d'un astre.

En revanche la force d'attraction de l'astre sur l'objet en orbite doit être la force prépondérante. C'est-à-dire que toutes les autres forces appliquées sur l'objet en orbite doivent être négligeables par rapport à la force d'attraction de l'astre sur l'objet en orbite.

On peut citer par exemple le satellite SOHO chargé d’observer en continu le Soleil afin d’en étudier la structure interne, les processus produisant le vent solaire ainsi que la couronne solaire.

Lois des aires - source : Maxicours

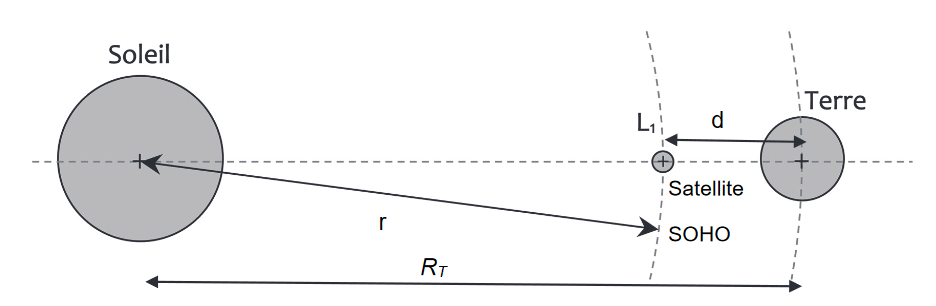
Le satellite est placé sur une orbite autour du Soleil ; le Soleil, le satellite et la Terre sont alignés à tout instant, afin que la Terre ne vienne jamais éclipser la lumière du Soleil par rapport au satellite. Celui-ci possède alors la même période de révolution que la Terre, alors que l'éllipse qu'il parcourt n'a pas le même demi grand-axe que celle de la Terre.

Dans ce cas, la 3ème loi de Kepler n'est pas respectée. En effet dans la relation $\frac{T^2}{a^3}=\text{constante}$, pour une même période $T$, $a$ ne peut pas être différent.