Méthode de résolution de problème

Dans cette partie, nous allons voir comment résoudre un problème de mécanique dans un champ uniforme. La résolution d'un problème de mécanique dans un champ uniforme mobilise de nombreuses notions, il est donc important de suivre une méthode rigoureuse pour ne rien oublier.

Le problème qui suit se veut volontairement complexe, sur le nombres de forces appliquées notamment, afin de se concentrer sur les méthodes et non les résultats attendus, afin d'éviter les automatismes qui peuvent amener des erreurs (i.e. $\overrightarrow{a}=\overrightarrow{g}$ alors que le poids est négligé...)

Énoncé du problème

Exercice

Extrtait modifié de l'épreuve de spécialité de physique-chimie, Amérique du Nord, jour 2, 2023.

Le BMX (Bicycle Moto Cross) est une discipline cycliste née aux USA et importée en France dans les années 1980. La « Race », sport olympique depuis 2008, est une course qui se déroule sur une piste bosselée de longueur comprise entre 270 et 400 m. Huit pilotes partent d’une butte de départ surélevée et doivent terminer le tour le plus rapidement possible en franchissant plusieurs types d’obstacles.

Lorsque la grille s’abaisse, sur la piste possédant une butte de départ à $8m$ de hauteur et faisant un angle $\alpha$ de $45°$ avec l'horizontale, les pilotes pédalent intensément pour acquérir la plus grande vitesse possible au bas de la butte.

Pendant cette descente, on considère que le système {pilote + bicyclette}, assimilé à un point matériel de masse totale $m=93kg$ se déplace de la position A jusqu’à la position B, en étant soumis à quatres actions mécaniques modélisées par son poids $\overrightarrow{P}$, la force de frottement $\overrightarrow{f}$ supposée constante et parallèle au plan, la force de réaction du sol $\overrightarrow{R}$ toujours perpendiculaire au plan et la force motrice $\overrightarrow{F}$ supposée constante et parallèle au plan. Le référentiel terrestre est ici considéré comme galiléen.

Profil de la butte et forces appliquées au système à un instant quelconque

Données :

• intensité de la pesanteur : $g=9,81\mathrm{m}.{\mathrm{s}}^{-2}$
• théorème de l’énergie cinétique : la variation d’énergie cinétique d’un système entre deux positions A et B est égale à la somme des travaux des forces appliquées à ce système entre les deux positions A et B.

Poser le problème

Identifier le référentiel et le système étudié

Le référentiel est le système de coordonnées dans lequel on étudie le mouvement. On lui associe un repère, une base de vecteurs permettant les projections. Il est important de le définir car il permet de définir les vecteurs position, vitesse et accélération, etc.

Exercice

Ici le système est le système {pilote + bicyclette}, de masse $m$, dans le référentiel terrestre supposé galiléen, muni du repère $(O,\overrightarrow{i},\overrightarrow{k})$. Il est donc possible d'appliquer la deuxième loi de Newton.

Identifier les conditions initiales

Les conditions initiales permettent de déterminer l'état du système à l'instant initial $t=0s$.

Les coordonnées initiales du vecteur position $\overrightarrow{OM}(t=0)$ peuvent être données dans l'énoncé ou être déterminées graphiquement. Il en est de même pour le vecteur vitesse $\overrightarrow{v}(t=0)$. Dans l'énoncé, ces informations sont parfois implicites. Par exemple, si le système est "lâché sans vitesse initiale", alors cela signifie que $\overrightarrow{v}(t=0)=\overrightarrow{0}$.

Exercice

Ici, le système est lâché sans vitesse initiale. On a donc $\overrightarrow{v}(t=0)=\overrightarrow{0}$. Les coordonnées initiales du vecteur position $\overrightarrow{OM}(t=0)$ peuvent être déterminées graphiquement $\overrightarrow{OM}(t=0)=z_A\cdot \overrightarrow{k}$ avec $z_A=8m$.

$$\overrightarrow{OM}(t=0)=\left\{\begin{array}{c}{x}_0=0\\ z_0=z_A\end{array}\right\}$$$$\overrightarrow{v}(t=0)=\left\{\begin{array}{c}{v}_{x0}=0\\ v_{z0}=0\end{array}\right\}$$

Remarque : Il sera important de savoir projeter un vecteur sur un axe. En effet le vecteur vitesse intiale n'est pas toujours nul. Il peut être parallèle à un axe ou même former un angle avec un axe. La partie suivante sur le bilan des forces détaille ce point.

Faire un bilan des forces

Faire un bilan des forces permet de déterminer les forces qui s'appliquent sur le système. Il est important de prendre en compte toutes les forces qui s'appliquent sur le système. Certaines forces peuvent être négligées si elles sont très faibles devant les autres forces. Ces informations sont généralement données dans l'énoncé (par exemple, la "force de frottement peut être négligée", "on néglige le poids de l'électron devant la force électrostatique", etc.).

Exercice

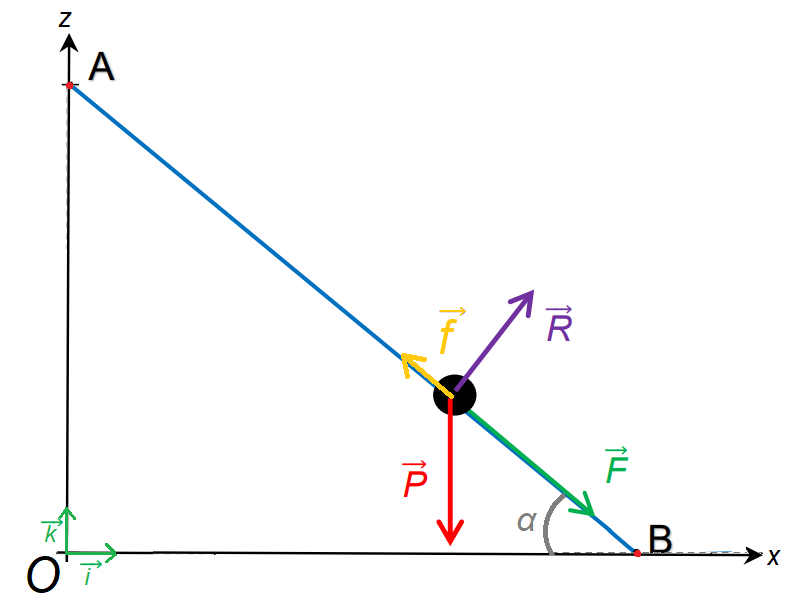
Ici, le système est soumis à quatre forces : le poids $\overrightarrow{P}$, la force de frottement $\overrightarrow{f}$, la force de réaction du sol $\overrightarrow{R}$ et la force motrice $\overrightarrow{F}$. La projection de ces forces sur les axes du repère permet de déterminer les composantes de ces forces. Comme pour la vitesse initiale, il est important de savoir projeter un vecteur sur un axe. Pour une meilleure visibilité des angles et des projections des vecteurs, voici le schéma du système annoté avec les angles :

Profil de la butte et forces appliquées au système à un instant quelconque annoté

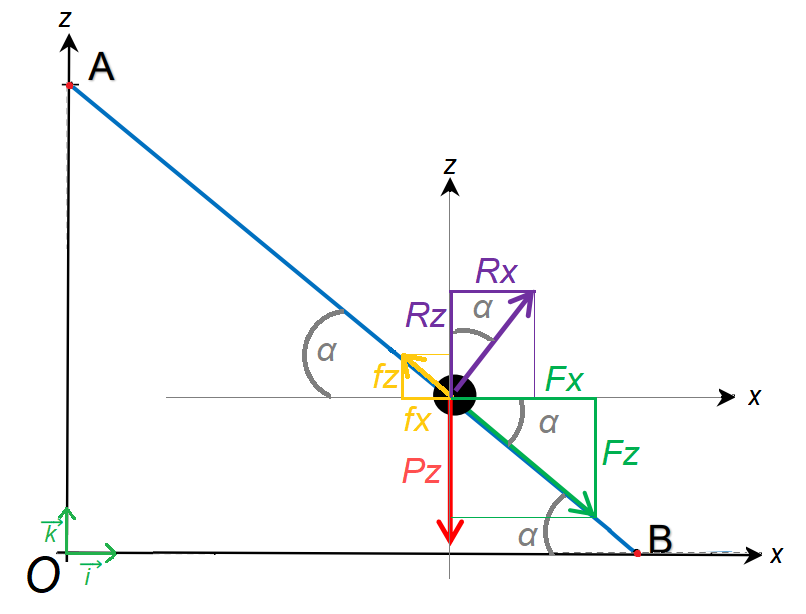
Remarques : Il est possible de placer les axes du repère au niveau du centre de masse afin de faciliter la lecture des projections. Savoir identifier tous les angles n'est pas exigible, ils seront donnés dans l'énoncé.

• Le poids $\overrightarrow{P}$ est une force verticale dirigée vers le bas. $\overrightarrow{P}=-m\cdot g\cdot \overrightarrow{k}$

$$\overrightarrow{P}=\left\{\begin{array}{c}{P}_x=0\\ P_z=-m\cdot g\end{array}\right\}$$

• La force de frottement $\overrightarrow{f}$ est une force parallèle au plan opposée au mouvement. $\overrightarrow{f}=-f\cdot cos(\alpha )\cdot \overrightarrow{i}+f\cdot sin(\alpha )\cdot \overrightarrow{k}$

$$\overrightarrow{f}=\left\{\begin{array}{c}{f}_x=-f\cdot cos(\alpha )\\ f_z=f\cdot sin(\alpha )\end{array}\right\}$$

• La force de réaction du sol $\overrightarrow{R}$ est une force perpendiculaire au plan. $\overrightarrow{R}=R\cdot sin(\alpha )\cdot \overrightarrow{i}+R\cdot cos(\alpha )\cdot \overrightarrow{k}$

$$\overrightarrow{R}=\left\{\begin{array}{c}{R}_x=R\cdot sin(\alpha )\\ R_z=R\cdot cos(\alpha )\end{array}\right\}$$

• La force motrice $\overrightarrow{F}$ est une force parallèle au plan dans le sens du mouvement. $\overrightarrow{F}=F\cdot cos(\alpha )\cdot \overrightarrow{i}-F\cdot sin(\alpha )\cdot \overrightarrow{k}$

$$\overrightarrow{F}=\left\{\begin{array}{c}{F}_x=F\cdot cos(\alpha )\\ F_z=-F\cdot sin(\alpha )\end{array}\right\}$$

Faire un schéma dans un état quelconque

Il peut être utile de faire un schéma dans un état quelconque du système non dans l'état initial. En effet certaines caractéristiques du système évoluent au cours du temps. Par exemple, un système peut avoir une vitesse nulle à l'instant initial et une vitesse non nulle à un instant quelconque.

Résoudre le problème

Pour résoudre le problème, il est possible d'utiliser une loi physique. On utilise généralement la deuxième loi de Newton, le théorème de l'énergie cinétique ou la conservation de l'énergie mécanique.

Deuxième loi de Newton - Equation horaire et de la trajectoire

La deuxième loi de Newton permet de déterminer les équations horaires du mouvement et l'équation de la trajectoire du système. Il ensuite possible de déterminer des positions particulières du système comme les positions d'équilibre, les positions d'arrêt, de déterminer la vitesse du système à un instant donné, etc.

Exercice

D'après la deuxième loi de Newton, on a :

$$\begin{array}{rl}\sum \overrightarrow{F_{ext}}& =m\cdot \overrightarrow{a}\\ \overrightarrow{P}+\overrightarrow{f}+\overrightarrow{R}+\overrightarrow{F}& =m\cdot \overrightarrow{a}\\ \frac{\overrightarrow{P}+\overrightarrow{f}+\overrightarrow{R}+\overrightarrow{F}}{m}& =\overrightarrow{a}\end{array}$$$$\overrightarrow{a}=\left\{\begin{array}{c}{a}_x=\frac{F_x+P_x+f_x+R_x}{m}=\frac{F\cdot cos(\alpha )-f\cdot cos(\alpha )+R\cdot sin(\alpha )}{m}=\frac{(F-f)\cdot cos(\alpha )+R\cdot sin(\alpha )}{m}\\ a_z=\frac{F_z+P_z+f_z+R_z}{m}=\frac{-F\cdot sin(\alpha )-m\cdot g+f\cdot sin(\alpha )+R\cdot cos(\alpha )}{m}=\frac{(-F+f)\cdot sin(\alpha )+R\cdot cos(\alpha )-m\cdot g}{m}\end{array}\right\}$$

Remarque : Les coordonnées semblent à première vue compliquées, mais il s'agit seulement de constantes. On pourrait par exemple continuer à utiliser $a_x$ et $a_z$ dans la suite du problème et simplement développer les expressions de ces coordonnées lorsqu'on en a besoin.

En déterminant la primitive des équations horaires de l'accélération, on obtient les équations horaires de la vitesse :

$$\overrightarrow{v}(t)=\left\{\begin{array}{c}{v}_x(t)=\frac{(F-f)\cdot cos(\alpha )+R\cdot sin(\alpha )}{m}\cdot t+v_{x0}\\ v_z(t)=\frac{(-F+f)\cdot sin(\alpha )+R\cdot cos(\alpha )-m\cdot g}{m}\cdot t+v_{z0}\end{array}\right\}$$

Or $\overrightarrow{v}(t=0)=\overrightarrow{0}$, donc $v_{x0}=0$ et $v_{z0}=0$.

$$\overrightarrow{v}(t)=\left\{\begin{array}{c}{v}_x(t)=\frac{(F-f)\cdot cos(\alpha )+R\cdot sin(\alpha )}{m}\cdot t\\ v_z(t)=\frac{(-F+f)\cdot sin(\alpha )+R\cdot cos(\alpha )-m\cdot g}{m}\cdot t\end{array}\right\}$$

En déterminant la primitive des équations horaires de la vitesse, on obtient les équations horaires de la position :

$$\overrightarrow{OM}(t)=\left\{\begin{array}{c}x(t)=\frac{(F-f)\cdot cos(\alpha )+R\cdot sin(\alpha )}{2\cdot m}\cdot t^2+x_0\\ z(t)=\frac{(-F+f)\cdot sin(\alpha )+R\cdot cos(\alpha )-m\cdot g}{2\cdot m}\cdot t^2+z_0\end{array}\right\}$$

Or $\overrightarrow{OM}(t=0)={\overrightarrow{OM}}_0$, donc $x_0=0$ et $z_0=z_A$.

$$\overrightarrow{OM}(t)=\left\{\begin{array}{c}x(t)=\frac{(F-f)\cdot cos(\alpha )+R\cdot sin(\alpha )}{2\cdot m}\cdot t^2\\ z(t)=\frac{(-F+f)\cdot sin(\alpha )+R\cdot cos(\alpha )-m\cdot g}{2\cdot m}\cdot t^2+z_A\end{array}\right\}$$

A partir des équations horaires de la position, on peut déterminer l'équation de la trajectoire. Pour cela, on exprime $t$ en fonction de $x$ (ou $z$) et on remplace dans l'autre équation. On obtient alors l'équation de la trajectoire.

$$\begin{array}{rl}x(t)& =\frac{(F-f)\cdot cos(\alpha )+R\cdot sin(\alpha )}{2\cdot m}\cdot t^2\\ \iff t& =\sqrt{\frac{2\cdot m\cdot x}{(F-f)\cdot cos(\alpha )+R\cdot sin(\alpha )}}\\ z(t)& =\frac{(-F+f)\cdot sin(\alpha )+R\cdot cos(\alpha )-m\cdot g}{2\cdot m}\cdot t^2+z_A\\ \iff z(x)& =\frac{(-F+f)\cdot sin(\alpha )+R\cdot cos(\alpha )-m\cdot g}{2\cdot m}\cdot \frac{2\cdot m\cdot x}{(F-f)\cdot cos(\alpha )+R\cdot sin(\alpha )}+z_A\\ \iff z(x)& =\frac{(-F+f)\cdot sin(\alpha )+R\cdot cos(\alpha )-m\cdot g}{(F-f)\cdot cos(\alpha )+R\cdot sin(\alpha )}\cdot x+z_A\end{array}$$

Théorème de l'énergie cinétique

Le théorème de l'énergie cinétique permet de déterminer l'évolution de l'énergie cinétique du système et de relier cette évolution aux travaux des forces appliquées au système. Il est ensuite possible de déterminer la vitesse du système à un instant donné ou en un point donné par exemple.

Exercice

D'après le théorème de l'énergie cinétique, on a :

$$\begin{array}{rl}\mathrm{\Delta }{E}_c& =\sum W(\overrightarrow{F_{ext}})\\ & =W(\overrightarrow{P})+W(\overrightarrow{f})+W(\overrightarrow{R})+W(\overrightarrow{F})\\ & =\overrightarrow{P}\cdot \overrightarrow{AB}+\overrightarrow{f}\cdot \overrightarrow{AB}+\overrightarrow{R}\cdot \overrightarrow{AB}+\overrightarrow{F}\cdot \overrightarrow{AB}\\ & =P\cdot AB\cdot cos(90°-\alpha )-f\cdot AB+0+F\cdot AB\\ & =(mg\cdot cos(90°-\alpha )-f+F)\cdot AB\end{array}$$

Remarque : $cos(90°-\alpha )=sin(\alpha )$ donc $\mathrm{\Delta }{E}_c=(mg\cdot sin(\alpha )-f+F)\cdot AB$.

Sachant que $\overrightarrow{v}(t=0)=\overrightarrow{0}$, on a $v_A=0$ et donc $E_{cA}=0$.

$$\begin{array}{rl}\mathrm{\Delta }{E}_c& =(mg\cdot sin(\alpha )-f+F)\cdot AB\\ E_{cB}-E_{cA}& =(mg\cdot sin(\alpha )-f+F)\cdot AB\\ E_{cB}& =(mg\cdot sin(\alpha )-f+F)\cdot AB\\ \frac{1}{2}\cdot m\cdot v_B^2& =(mg\cdot sin(\alpha )-f+F)\cdot AB\end{array}$$

Exploiter les résultats

Lors de l'exploitation des résultats, on peut être amené à :

• indiquer la nature d'un mouvement (rectiligne uniforme, rectiligne uniformément varié, circulaire uniforme, etc.)
• calculer des grandeurs spécifiques (durée d'un parcours, position particulière, vitesse en un point particulier, etc.)
• commenter, comparer des résultats (influence réelles des frotttements, etc.)

Exercice

• Le mouvement est uniformément varié car l'accélération est constante, non nulle $(|\overrightarrow{a}|=\sqrt{a_x^2+a_z^2}\ne 0)$. Il est rectiligne car la trajectoire est une droite $(z(x)=a\cdot x+b)$.

• Déterminer la durée $\mathrm{\Delta }t$ du parcours $AB$ :

  On sait que $t_A=0s$, et donc $\mathrm{\Delta }t=t_B$. De plus $z(t_B)=0m$. On peut donc déterminer $t_B$ en résolvant l'équation $z(t_B)=0m$.

  $$\begin{array}{rl}z(t_B)& =\frac{(-F+f)\cdot sin(\alpha )+R\cdot cos(\alpha )-m\cdot g}{2\cdot m}\cdot t_B^2+z_A\\ \iff 0& =\frac{(-F+f)\cdot sin(\alpha )+R\cdot cos(\alpha )-m\cdot g}{2\cdot m}\cdot t_B^2+z_A\\ \iff t_B& =\sqrt{\frac{-2\cdot m\cdot z_A}{(-F+f)\cdot sin(\alpha )+R\cdot cos(\alpha )-m\cdot g}}\end{array}$$

  Il est possible de déterminer $\mathrm{\Delta }t$ si l'on connait les valeurs des forces $F$, $f$, $R$, de $m$, $g$, $z_A$ et $\alpha$.

• Déterminer la vitesse $v_B$ du système à la position $B$ :

  • On peut déterminer la vitesse $v_B$ en utilisant les équations horaires de la vitesse sachant que $v_B=v(t_B)=\sqrt{v_x(t_B{)}^2+v_z(t_B{)}^2}$. Il est possible de déterminer $v_B$ si l'on connait les valeurs de $t_B$, des forces $F$, $f$, $R$, de $m$, $g$, $z_A$ et $\alpha$.

  • On peut sinon déterminer la vitesse $v_B$ en utilisant le théorème de l'énergie cinétique sachant que $\frac{1}{2}\cdot m\cdot v_B^2=(mg\cdot sin(\alpha )-f+F)\cdot AB$. On obtient alors $v_B=\sqrt{\frac{2\cdot (mg\cdot sin(\alpha )-f+F)\cdot AB}{m}}$. Il est possible de déterminer $v_B$ si l'on connait les valeurs de la longueur du parcours $AB$, des forces $F$, $f$, $R$, de $m$, $g$, $z_A$ et $\alpha$.

• Connaissant le temps de parcours $t_B$, déterminer l'intensité de la force de frottement $f$ :

  On sait que $z(t_B)=0m$. On peut donc déterminer $f$ en résolvant l'équation $z(t_B)=0m$.

  $$\begin{array}{rl}z(t_B)& =\frac{(-F+f)\cdot sin(\alpha )+R\cdot cos(\alpha )-m\cdot g}{2\cdot m}\cdot t_B^2+z_A\\ \iff 0& =\frac{(-F+f)\cdot sin(\alpha )+R\cdot cos(\alpha )-m\cdot g}{2\cdot m}\cdot t_B^2+z_A\\ \iff f& =\frac{-2\cdot m\cdot z_A}{t_B^2\cdot sin(\alpha )}+\frac{m\cdot g-R\cdot cos(\alpha )}{sin(\alpha )}+F\end{array}$$

  Il est possible de déterminer $f$ si l'on connait les valeurs de $t_B$, des forces $F$, $R$, de $m$, $g$, $z_A$ et $\alpha$.

Les exemples ci-dessus ne sont pas exhaustifs. Il est possible de déterminer d'autres grandeurs comme la position du système à un instant donné, la vitesse du système à un instant donné, etc. Il est important d'identifier les lois physiques qui permettent de déterminer les grandeurs recherchées. Il est possible de déterminer une grandeur à partir de plusieurs lois physiques, mais généralement la loi à utiliser sera précisée dans l'énoncé ("En utilisant la deuxième loi de Newton, déterminer ...", "En appliquant le théorème de l'énergie cinétique, déterminer ...", etc.).

Attention

Il faut bien travailler le cours, les différentes lois physiques et les différents outils à votre disposition. C'est l'étape la plus importante pour comprendre et résoudre un problème.

Evidemment il est également important de travailler la technicité mathématique. Il faut être capable d'isoler une grandeur dont on veut déterminer la valeur, de résoudre des équations du second degré (on a souvent des équations du type $z(t)=\frac{1}{2}\cdot g\cdot t^2+v_{z0}\cdot t+z_0$), etc. Mais cette technicité vous sera inutile si vous ne comprenez pas le problème qui vous est posé.